Angular kinetics
Angular kinetics investigates the causes of angular motion, or rotation. The turning effect of a force applied to a body is called torque. Torque is produced when a force is applied to a body at some distance from an axis of rotation (figure 8).
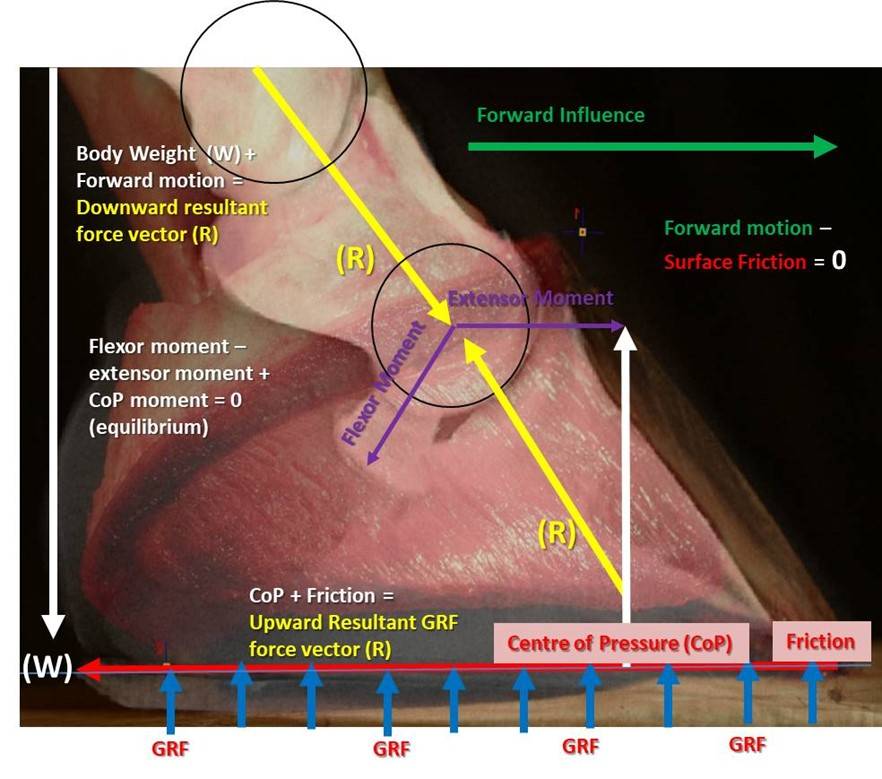
To describe movement, bio mechanists use a spatial reference system. All three dimensional structures, such as a horses foot, have three axis each of which has two coordinates. The three axes intersect at right angles to each other at the body or body segments centre of mass or balance point (CoP).The origin is at the intersection of the horizontal, mediolateral and vertical axes and is designated as zero (0) (figure?).
Looking for the Hypotenuse
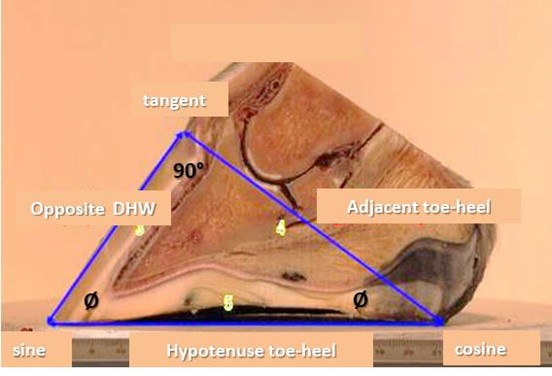
Some basic principles from geometry such as Pythagoras’s theory are very important in biomechanics. The right-angle triangle) is a useful figure when working problems in biomechanics, because the relationships among the lengths of the sides of the right triangle. This relates to how farriers provide a toolbox for not only working with vectors such as the optimum length of shoe. The side across from the 90-degree angle in a right triangle is called the hypotenuse. The hypotenuse is always the longest side of the triangle. In all triangles, the sum of the three angles is 180 degrees. Because one angle in a right triangle is 90 degrees, the sum of the other two angles is obviously 90 degrees. Each of these two other angles is less than 90 degrees; angles less than 90 degrees are called acute angles (figure 8).
Using Trigonometry
Trigonometry is the field of mathematics describing the relationship between the sides and angles of triangles. Just as Pythagoras’s theory allows you to calculate the optimum length of a shoe for example, the trigonometric functions allow you to calculate the length, and any necessary elevations required, of the sides of a right triangle if the length of one side and the measure of one acute angle are known. One of example of this is in calculating the size of elevation and the length of the hypotenuse (shoe) to achieve an effective right angled triangle for feet exhibiting collapsed weak heels.
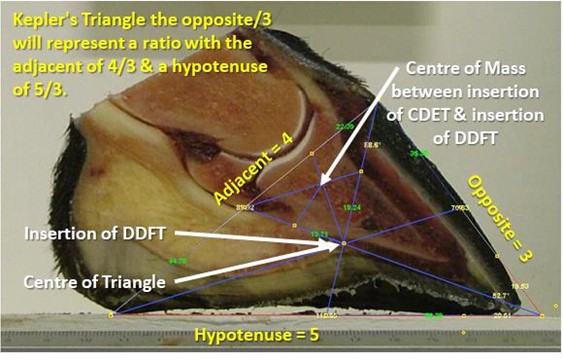
The trig functions specify the ratios between two sides of the right triangle. A ratio is the relationship between two measurable quantities. Many farriers might be familiar with the so called “Golden Ratio” (1.618), which is often cited in articles on the subject of foot balance, made famous by Leonardo da Vinci’s “Vitruvian Man” in 1490. An example of the use of maths in understanding farriery theory was demonstrated in a recent study on foot geometry by Balchin (2012). The study suggested that geometric proportions may be present within the sample of feet in the tested. 19 off 25 feet examined revealed the right angle triangle had edge lengths in the geometric progression known to form “Kepler’s Triangle”, which has its roots based in the theorem of Pythagoras and the Golden Ratio, it was interesting to note that the centre of the triangle was located at the point where the Deep Digital Flexor Tendon inserts into the semi lunar crest on the solar surface of the Distal Phalanx, and equally as interesting is the fact that once the triangle and ratio are in position then another Golden ratio and Kepler’s Triangle are formed. The smaller triangle and ratio are clearly visible in figure? And It would appear that the centre of this triangle represents the centre of mass within the foot segment (figure 9).
Figure 9 below Shows the Tangent of the right angle triangle is from the hairline of the coronary band and the Sine is at the bearing border of the toe. This means that the Cosine will be situated at or within millimetres of the last weight bearing point of the heel. The Hypotenuse is then formed by the bearing border of the foot with the Opposite being formed by the Dorsal wall whilst the Adjacent was formed by the line from the Tangent to the Cosine or the hairline at the Coronary band to the last weight bearing point of the heel.
Vector Quantities
In biomechanics, two types of quantities are important:
Scalars: A scalar is any quantity that can be fully described by its magnitude, size, or amount for example time, mass, distance, and speed (figure 10). A scalar quantity is fully described the specific number of units used to measure it — for example, time = 8 seconds (or s), mass = 75 kg, distance = 2 m, or speed = 20 m/s.
Vectors: A vector is described not just by its magnitude but also by a direction associated with the quantity (figure 11). Vector quantities include force, displacement, velocity, and acceleration and are only fully described if both magnitude and direction are specified — for example, force = 20 Newtons (N) to the right. For example; displacement = 5 m at an angle of 40 degrees to the horizontal, velocity = 5 m/s at an angle of 20 degrees to the horizontal, or acceleration = 10 m/s/s downward. A vector quantity is graphically represented by an arrow called, simply, a vector. A vector is drawn so the magnitude of the quantity is represented by the length of the arrow, and the direction of the quantity is represented by the tip, or arrowhead.
Vector resolution: Vectors can be resolved into components, typically a horizontal component and a vertical component (often called the x and y components) acting at 90 degrees to each other. This process applies the trigonometric functions, described earlier, of the sine, cosine, and tangent. Vector composition allows for the combination of two separate vectors into a single resultant vector. A resultant represents the combined effect of the two vectors (figure 11).

- Kinematics: the Science of Movement.
Kinematics isn’t concerned with the forces that cause the movement but is the branch of mechanics that describes motion including any change in position of a body over a period of time. Kinematics describes the spatial (movement through space) and temporal (timing) aspects of movement; it. The kinematic description of movement is the details of what is seen studying performance. The basic spatial measures in kinematics include where, how far, how fast, and whether the body is speeding up or slowing down. The timing measures include when, how long, and the sequencing of the component parts of the movement, including the sequential joint actions.
All movement can be classified as either linear or angular:
Linear motion: Linear motion occurs when all parts of a body or segment experience the same change in position during the same period of time. There are two types of linear motion.
I. Rectilinear motion is motion in a straight line. All points on the body move exactly the same, and the orientation of the body does not change.
II. Curvilinear motion is motion along a curved path. The body is moving simultaneously in two (or three) different planes. For example, when the foot is in the swing phase of the stride it follows a curvilinear path through the air. It moves up and then down at the same time that it moves away from you. This simultaneous movement in two different directions creates what is termed a parabolic path. The foot and limb can also be moving sideways along with the up–down and a forward path through the air but it still follows a parabolic path.
Angular motion: Angular motion is the formal name for rotation — twists, spins, and turns. Rotation occurs when all points on the body go through the same angle. A point farther from the axis of rotation travels through the same angle as a point closer to the axis of rotation, but the curvilinear path travelled by a point farther from the axis of rotation is longer than the curvilinear path travelled by a point closer to the axis of rotation. The whole body can rotate, and the individual segments of the body rotate at the joints.
- General motion — a combination of angular motion and linear motion and is the most common form of motion. The linear motion of a point on a segment can only undergo linear motion because of a coordinated combination of angular motion at two or more joints. Synchronizing the angular motion of joints is a critical factor for successful performance,

Describing how far: Distance and displacement
The terms distance and displacement are often used interchangeably in everyday conversation. Both terms describe how far a body moves. However, they have specific, and different, definitions in mechanics. Distance and displacement are measured in both linear and angular kinematics.
Distance
Distance is a scaler that simply describes how far the body moved during a time interval. Distance includes all the movement of the body from the start to the end of the motion, regardless of whether the body changes direction while traveling. Linear distance is defined as the length of the total travelled by a body, and it is measured in meters (m). How far the body moves and how long it takes to move affect the calculation of how fast. How fast a body moves depends on whether how far is measured as a distance or as a displacement.
Angular distance is equal to the entire length of the angle travelled between the first and the final angular positions and is measured in degrees (°). Angles are sometimes measured in radian (1 radian = 57.3 degrees).
Speed simply describes how fast the body moved when it travelled the measured distance. You calculate speed by dividing the length of the path travelled by the length of time. In other words, speed = distance/time .
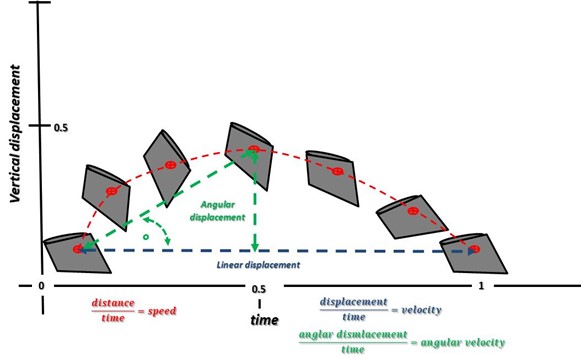
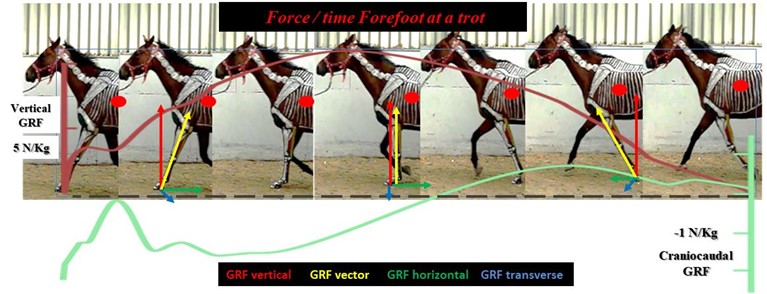
Velocity is a vector and describes how fast a body moved when it underwent a specific displacement. Velocity is calculated by dividing displacement by the length of time (figure?). Linear velocity is calculated as linear displacement divided by time and angular velocity is calculated as angular displacement divided by time. In describing either linear velocity or angular velocity, the direction of the body’s motion is also specified.
Pushing and Pulling into Kinetics
Kinetics is the branch of mechanics focused on the forces acting on a body. A force is a push or a pull created by the interaction of two bodies. Force is a vector quantity, and it’s described by the characteristics of magnitude (the size of the force) and the direction of the force. Two other important characteristics of a force are its point of application (where on the body the force is applied) and its line of action (an imaginary extension of the force vector in both directions, used to determine the torque, or turning effect, of the force). A familiar concept is seen in the shoe making process (figure 14) where both the magnitude of and the direction of the force are essential components of the process. Two other important characteristics of a force are its point of application (where on the material the force is applied) and its line of action (an imaginary extension of the force vector in both directions, used to determine the torque, or turning effect, of the force).

Inertia refers to a body’s resistance to changing its motion. Essentially, inertia means that when a body is at rest, it wants to stay at rest, and when a body is moving, it wants to continue to move at the same speed and in the same direction (the body tends to maintain its velocity). A good way to think of this is that when a limb is bearing a loading force another unopposed force, say muscular tension, must be acting on it. Inertia comes from the body’s mass is measured and reported as a single value of weight without considering each individual element within it.
The pushes and pulls on a body — the forces — are classified as either internal or external:
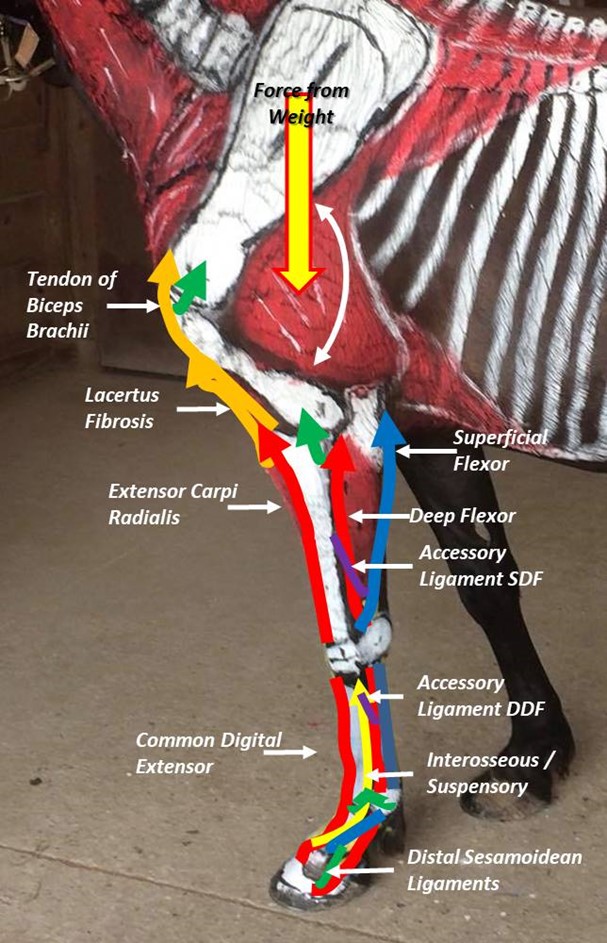
Internal force: A force produced within the body. An internal force doesn’t affect the motion of the body — an internal force does not cause an acceleration of the whole body. An internal force pushes or pulls on the parts within the body, causing a deformation of the material called strain, depending on the magnitude of the stress produced. (Stress is a measure of how the applied force is distributed over the internal structure of the body). When looking at the body as a whole, the pulling force of stay apparatus is an internal force (figure 15).
External force: A force applied to a body by something outside the body. External force acting on a body wants to change the motion of the body, to cause it to speed up or slow down (in other words, an external force wants to accelerate the body). We move around the environment because of the external forces that act on our bodies. We use our muscles to pull on our segments to produce external forces on our bodies.
External forces fall into two categories:
Non-contact force: A non-contact force occurs when the two bodies are not in contact with each other. The most common external force in biomechanics is weight. The weight of a body is caused by the pulling force of gravity. The weight of a body is calculated as the mass of the body multiplied by the acceleration of gravity, or W = mg, where
W is weight, m is the mass of the body (in kilograms), and g is the gravitational acceleration of –9.81 m/s/s. It’s important to remember that weight is a downward force. Because gravity pulls down on the body, weight always acts downward in the vertical direction. If the limb is moving in an upward direction the downward force of gravity acts to slow it down. When the limb is moving downward, weight acts to speed it up.
Contact force: A contact force occurs when two bodies touch. The force is created by the interaction of the two bodies. Sometimes the effect of the force is obvious, as when the foot impacts with the ground during movement. A contact force is present between the foot and the ground even when the horse is standing upright and not moving. Friction is a contact force present for example when the foot slides on the surface during deceleration; in this case friction always opposes the direction of the sliding. The factors affecting friction include the force squeezing the bodies together (called the normal force) and the materials in contact with each other where the sliding can occur (represented what is termed the coefficient of friction).
To be Continued in Part 3.
